반응형
문제 :
모평균이 50.2이고 모분산이 48인 어떤 모집단으로부터 크기가 100인 표본이 임의추출되었다고 할 때
표본평균이 47에서 51 사이에 있을 확률을 구해보자.
scipy.stats 에 보면, norm 이라는 클래스가 있다. 정규분포를 다룰 수 있는 클래스를 만들어준다. 정규분포는 평균과 표준편차 두 수치로 결정된다. norm 클래스 생성자 인자도 이 두개.
문제에서 표분평균의 표본분산은 모분사/표본크기 이고, 중심극한정리에 따라 정규분포를 따른다. N(x, m=502, sig^2=48/100) 을 구하면 된다.
구간의 확률은 norm 클래스의 cdf 함수의 차로 구할 수 있다.
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
import scipy.stats
def show_pdfcdf(rv, m, s):
mm = m
ss = 6 * s
xx = np.linspace(mm - ss, mm + ss, 200)
pdf = rv.pdf(xx)
cdf = rv.cdf(xx)
plt.grid(True)
plt.plot(xx, pdf)
plt.plot(xx, cdf)
plt.title(f" Norm(m={m}, s^2={s*s:.3f}) Pdf & Cdf ")
plt.savefig("dist.png")
plt.show()
m, s = 50.2, np.sqrt(48 / 100)
rv = sp.stats.norm(m, s)
show_pdfcdf(rv, m, s)
x1, x2 = 47, 51
print(f"Prob ({x1} < x < {x2}) =", rv.cdf(x2) - rv.cdf(x1))
중간의 plot 하는 부분은 문제풀이와는 사실 상관이 없는데, 그래도 그래프를 하나 그려 놓으면 내가 만든 결과가 대충 맞는지 확인해 볼 수 있으므로, 그려 보았다.
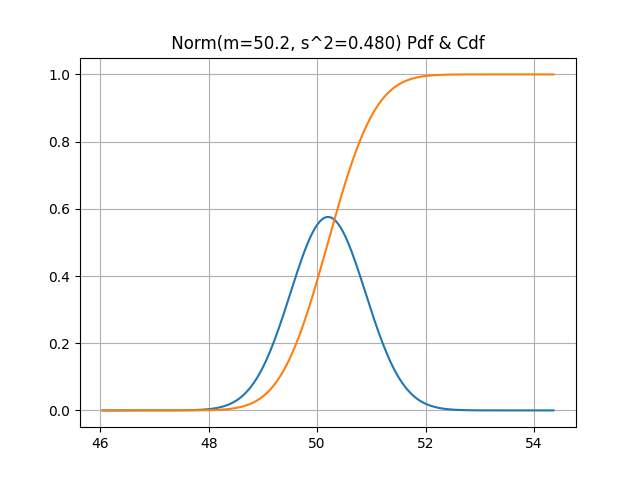
Prob (47 < x < 51) = 0.875891530696819결과는 위와 같다.
see also : 사이파이를 활용한 확률분석 (데싸스쿨)
728x90
'프로그래밍 > Python' 카테고리의 다른 글
| [Anaconda] conda install 과 pip install 은 똑같은 걸까? (0) | 2020.12.23 |
|---|---|
| [통계학|scipy] 정규분포 모집단의 표본분산의 분포는 정말 카이제곱분포를 따를까 (0) | 2020.12.22 |
| 윈도우용 파이썬 3.8 버전에서 pip install kivy 로 설치가 안 된다. (0) | 2020.12.09 |
| [Python] 윈도우 cmd 창에서 python 을 입력하면 윈도우 스토어 설치화면이 나온다. (0) | 2020.12.05 |
| [Python] 분수의 무제한 소수표현 구하기 (3) | 2020.12.04 |

