반응형
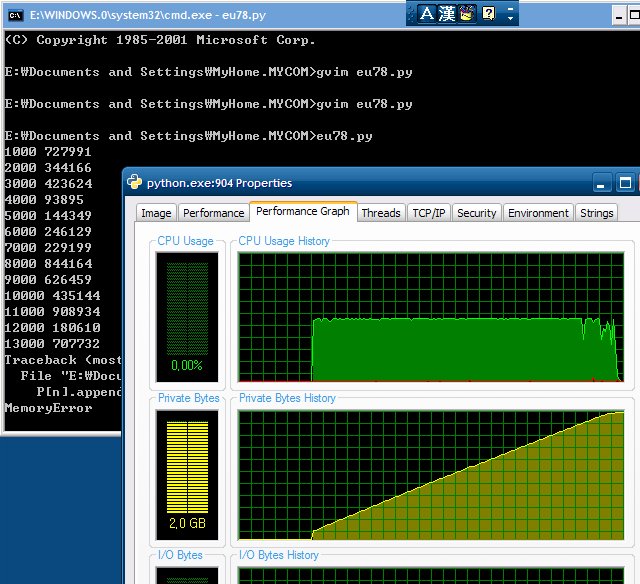
76, 77번을 풀었던 방법으로 풀었는데, 끝까지 계산하지 못하고 오버플로우가 났다. 삼각형 형태로 메모리가 늘어나서 13000 까지 찍고 죽는 것이었다. 그래서 위키백과의 점화식을 이용하여 푸는 코드를 짜서 풀었다. 점화식은 2차원인 아닌 1차원으로 기억하고 있으면 되서 답을 내 줬다.
죽는 코드와 죽는 모습
#!/usr/bin/env python
# euler 78
P = []
n = 0
P.append([])
P[n].append(0) # P[0][0]
n = 1
P.append([])
P[n].append(0) # P[1][0]
P[n].append(1) # P[1][1]
n = 2
while 1:
cnt = 0
P.append([])
for i in range(n+1):
if i == 0:
cnt = 0
elif i == n:
cnt += 1
else:
#print('--')
#print(n-i, i)
if i > n-i:
cnt += P[n-i][n-i]
else:
cnt += P[n-i][i]
cnt %= 1000000
P[n].append(cnt)
# print('==========')
# for pn in P:
# print(pn)
# if cnt > 40:
# break
if n % 1000 == 0:
print(n, P[n][n])
if P[n][n] % 1000000 == 0:
break
n+=1
print(n, P[n][n])
답을 내준 코드 결과는 답과 살짝 틀리다.
#!/usr/bin/env python
#
# wikipedia : Partition Function
# http://en.wikipedia.org/wiki/Partition_function_%28number_theory%29
#
# p(k) = p(k - 1) + p(k - 2) - p(k - 5) - p(k - 7) + p(k - 12) + p(k - 15) - p(k - 22)...
#
# where the sum is taken over all generalized pentagonal numbers of the form n(3n - 1)/2.
#
#
p = [ 0 , 1 ] # p[0] is place-holder
k = 2
while 1 :
pn = 0
i = 1
ii = 2
while 1:
kk = int(k - i*(3*i-1)/2)
#print(k, i, kk, k-kk)
if kk < 1:
break
if ii%4 == 2 or ii%4 == 3:
pn += p[kk]
else:
pn -= p[kk]
if ii%2 == 1:
i+=ii
else:
i-=ii
ii+=1
p.append(pn)
# if k > 10:
# break
if pn%1000000 == 0:
break
k += 1
print(k, p[k])
#print(p)
죽는 코드와 죽는 모습
#!/usr/bin/env python
# euler 78
P = []
n = 0
P.append([])
P[n].append(0) # P[0][0]
n = 1
P.append([])
P[n].append(0) # P[1][0]
P[n].append(1) # P[1][1]
n = 2
while 1:
cnt = 0
P.append([])
for i in range(n+1):
if i == 0:
cnt = 0
elif i == n:
cnt += 1
else:
#print('--')
#print(n-i, i)
if i > n-i:
cnt += P[n-i][n-i]
else:
cnt += P[n-i][i]
cnt %= 1000000
P[n].append(cnt)
# print('==========')
# for pn in P:
# print(pn)
# if cnt > 40:
# break
if n % 1000 == 0:
print(n, P[n][n])
if P[n][n] % 1000000 == 0:
break
n+=1
print(n, P[n][n])
답을 내준 코드 결과는 답과 살짝 틀리다.
#!/usr/bin/env python
#
# wikipedia : Partition Function
# http://en.wikipedia.org/wiki/Partition_function_%28number_theory%29
#
# p(k) = p(k - 1) + p(k - 2) - p(k - 5) - p(k - 7) + p(k - 12) + p(k - 15) - p(k - 22)...
#
# where the sum is taken over all generalized pentagonal numbers of the form n(3n - 1)/2.
#
#
p = [ 0 , 1 ] # p[0] is place-holder
k = 2
while 1 :
pn = 0
i = 1
ii = 2
while 1:
kk = int(k - i*(3*i-1)/2)
#print(k, i, kk, k-kk)
if kk < 1:
break
if ii%4 == 2 or ii%4 == 3:
pn += p[kk]
else:
pn -= p[kk]
if ii%2 == 1:
i+=ii
else:
i-=ii
ii+=1
p.append(pn)
# if k > 10:
# break
if pn%1000000 == 0:
break
k += 1
print(k, p[k])
#print(p)
728x90
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [Euler Project 164] 연속된 세 개의 자리수의 합이 9를 넘지 않는 20자리수 (0) | 2011.05.11 |
|---|---|
| 생성함수 (0) | 2009.08.14 |
| [Euler Project 077] 소수의 합으로 표현하는 가짓수 (0) | 2009.08.01 |
| [Euler Project 203] 소수제곱없는 이항계수의 합 구하기 (0) | 2009.07.30 |
| [Euler Project 101] 수열 다항식으로 근사하기 (0) | 2009.07.26 |