반응형
# http://projecteuler.net
# Problem 92
# 2 2 2 2 2
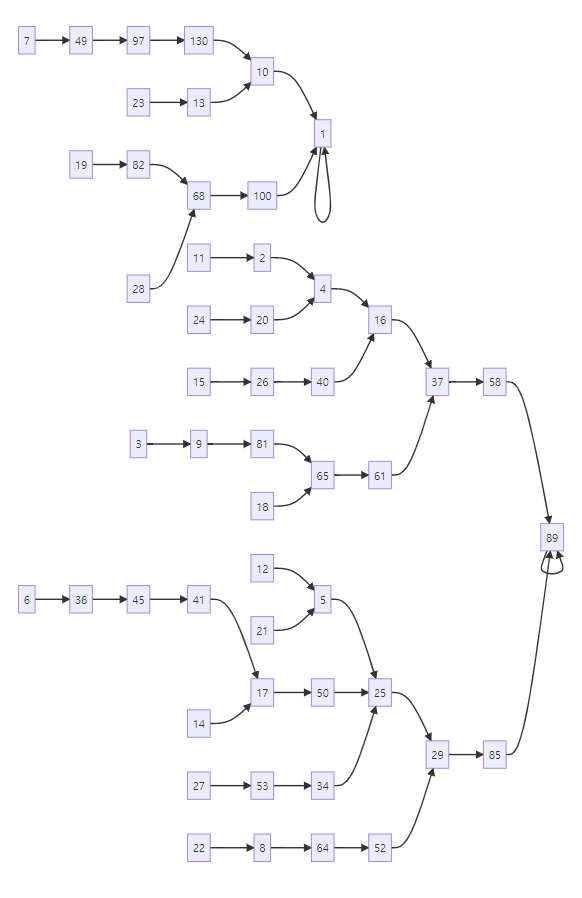
# 89 -> 8 + 9 = 145 -> 1 + 4 + 5 = 42 -> 20 -> 16 -> 37 -> 58 -> 89 -> ... -> 89
# 1 -> 1 -> 1
from functools import lru_cache
import time
from tqdm import tqdm
BIGN = 10 ** 7
sol_dict = dict()
sol_dict[0] = 0
sol_dict[1] = 1
sol_dict[89] = 89
digit_sq = [i * i for i in range(10)]
@lru_cache
def arrives_at_89_recur(n: int):
if n == 0 or n == 1 or n == 89:
return n
digit_square_sum = 0
while n > 0:
digit = n % 10
digit_square_sum += digit_sq[digit]
n //= 10
return arrives_at_89_recur(digit_square_sum)
def arrives_at_89(n):
chain = []
while 1:
if sol_dict.get(n, -1) != -1:
for i in chain:
sol_dict[i] = sol_dict[n]
break
next = 0
while n > 0:
digit = n % 10
next += digit_sq[digit]
n //= 10
n = next
chain.append(n)
# print next,
return sol_dict[n]
cnt = 0
t0 = time.time()
for i in tqdm(range(BIGN)):
if arrives_at_89_recur(i) == 89:
cnt += 1
dt = time.time() - t0
print(cnt)
print(f"took {dt:.3f} seconds")
cnt = 0
t0 = time.time()
for i in tqdm(range(BIGN)):
if arrives_at_89(i) == 89:
cnt += 1
dt = time.time() - t0
print(cnt)
print(f"took {dt:.3f} seconds")
lru_cache 로 재귀함수를 만들어서도 풀어 봤고, 딕셔너리로 캐시를 만들고, 재귀가 아닌 함수를 만들어서도 풀어 보았다. 과거에 풀었던 것은 다시 풀었는데, 과거에는 캐시를 만드는 아이디어는 동일했지만, 캐시를 -1로 초기화된 리스트로 구성했었기 때문에, 메모리잡는데에만도 시간이 많이 걸렸었다. 또한 캐시를 세팅하는 부분에도 버그가 있어서 캐시를 제대로 이용하지 못했었다.
내 피씨에서 실행하여 시간을 비교해 보니 lru_cache 가 30-35초, 내가만든 캐시가 20-25초 정도 걸리는 걸 확인할 수 있었다.
728x90
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [EP003] 큰 수의 소수분해 (0) | 2020.11.23 |
|---|---|
| [EP 023] 두 과잉수의 합으로 나타낼 수 없는 모든 수의 합 (0) | 2020.11.23 |
| [EP 005] least common multiple for a list of numbers (0) | 2020.11.18 |
| [EP 080] 100까지의 정수의 제곱근의 자리수 합 (0) | 2020.11.17 |
| [파이썬] 이집트분수 (0) | 2020.04.23 |