직육면체가 특정 면으로 착지할 확률

관련 포스팅

http://astralepic.egloos.com/4022771
http://zariski.egloos.com/2229177
http://mcfrog.org/tt/848

#!/usr/bin/env python

import math

def length(V):
    sq_sum = 0
    for i in xrange(3):
        sq_sum += V[i]*V[i]
    return math.sqrt(sq_sum)

def dot(U, V):
    d = 0
    for i in xrange(3):
        d += U[i]*V[i]
    return d

def omega(A, B, C):
    ''' computes the steradian defined by three vectors A, B, C.

    ref : http://en.wikipedia.org/wiki/Solid_angle
    Oosterom and Strackee

          1                        A . B x C 
    tan( --- omega ) = --------------------------------
          2             abc + (A.B)c + (B.C)a + (C.A)b

                        /            A . B x C           \ 
    omega = 2 * arctan |  ------------------------------  |
                        \ abc + (A.B)c + (B.C)a + (C.A)b /
    '''
    detABC = ((A[0]*B[1]*C[2] + A[1]*B[2]*C[0] + A[2]*B[0]*C[1])
            - (A[2]*B[1]*C[0] + A[1]*B[0]*C[2] + A[0]*B[2]*C[1]))
    a = length(A)
    b = length(B)
    c = length(C)
    AB = dot(A,B)
    BC = dot(B,C)
    CA = dot(C,A)
    tanhalf = detABC / ( a*b*c + AB*c + BC*a + CA*b )
    sr = math.atan(tanhalf)*2
    return math.fabs(sr) # positive

def prob(a, b, c):
    ''' computes three relative steradians '''
    sab = omega([0, 0, 1], [0, b, c], [a, b, c]) + omega([0, 0, 1], [a, 0, c], [a, b, c])
    sbc = omega([1, 0, 0], [a, 0, c], [a, b, c]) + omega([1, 0, 0], [a, b, 0], [a, b, c])
    sca = omega([0, 1, 0], [0, b, c], [a, b, c]) + omega([0, 1, 0], [a, b, 0], [a, b, c])
    return sab*2/math.pi, sbc*2/math.pi, sca*2/math.pi , (sab + sbc + sca)*2/math.pi

#print omega([1, 0, 0], [0, 1, 0], [0, 0, 1])/math.pi
#print omega([1, 1, 1], [0, 1, 0], [0, 0, 1])/math.pi
print prob(31, 13, 23)
print prob(1, 1, 1)

이렇게 생각해 보자. 직육면체는 모든 꼭지점에 대해 대칭성을 갖는다. 따라서, 운동에너지가 완전히 0이 되었을 때 바닥에 닿아 있는 꼭지점이 어느 것이든 상관없다. 이 때 바닥에 수직한 단위 벡터 N이 가질 수 있는 공간은 꼭지점을 중심으로하는 단위구의 1/8 (면적은 pi/2)이다. 단위구에서 직육면체의 대각선이 뚫고 지나가는 점과 8분의 구의 각 꼭지점을 지나는 세 개의 대원으로 나누어진 6개의 구간 중에 N이 어디에 위치하느냐에 따라 일단 어느면으로 떨어지느냐가 결정된다.

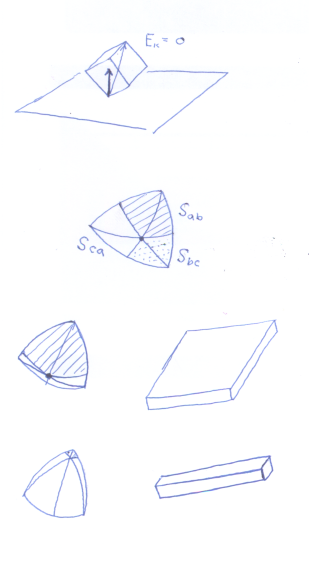
그걸 계산해 봤다.

0.25862878008027879, 0.14802647891057574, 0.59334474100914558